Abstract:  We present a consistent and conservative numerical method for solving the Navier-Stokes equations in flow domains that may be separated by any number of material interfaces, at arbitrarily-high density/viscosity ratios and acoustic-impedance mismatches, subjected to strong shock waves and flow speeds that can range from highly supersonic to near-zero Mach numbers. A principal aim is prediction of interfacial instabilities under superposition of multiple potentially-active modes (Rayleigh-Taylor, Kelvin-Helmholtz, Richtmyer-Meshkov) as found for example with shock-driven, immersed fluid bodies (oblique shocks)—accordingly we emphasize fidelity supported by physics-based validation, including experiments. Consistency is achieved by satisfying the jump-discontinuities at the interface within a conservative 2nd-order scheme that is coupled, in a conservative manner, to the bulk-fluid motions. The jump-conditions are embedded into a Riemann problem, solved exactly to provide the pressures and velocities along the interface, which is tracked by a level set function to accuracy at least 3rd-order. Subgrid representation of the interface is improved by allowing curvature of its constituent interfacial elements to obtain 3rd-order accuracy in cut-cell volume, with attendant benefits in calculating cell- geometric features and interface curvature. Overall the computation converges as 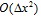. Spurious-currents are down to machine error and there is no time-step restriction due to surface tension. Our method is supported by an octree-based adaptive mesh refinement infrastructure. When necessary, this is supplemented by body-fitted grids to enhance resolution of the gas dynamics, including flow separation, shear layers, slip lines, and critical layers. Comprehensive comparisons with exact solutions for the Rayleigh-Taylor and Kelvin-Helmholtz problems demonstrate excellent performance. Sample simulations of liquid drops subjected to shock waves demonstrate for the first time ab initio numerical prediction of the key interfacial features and phenomena found in recent experimental and theoretical studies of this class of problems. [Theofanous, Ann. Rev. Fluid Mech. 43, 163-190, 2011].

About the Speaker

Dr. Chih-Hao Chang is currently an Associate Researcher in the Center of Risk Studies and Safety at University of California, Santa Barbara. Dr. Chang received his Ph.D. in aerospace engineering from National Cheng-Kung University, Taiwan in 1998. Before he joined UCSB in 2006, he had been working in Academia Sinica, NASA Glenn Center and University of Kentucky. His research interest is in numerical methods for multiphase flows under critical conditions, including free interface flow, hypervelocity disperse flow, explosive flow and interface instabilities for compressible flows.

DateTime: August 1, 2012 (Wednesday), 15:00 – 16:00
Location: 606 Conference Room