Extracting unbiased properties of quantum many-body systems exposes the challenge that numerical simulations in classical computers face in exploring quantum matter. Roughly put, one is trapped in a tale of two exponentials. On one side, a constraint arises due to the “exponential wall” associated with the growing dimension of the Hilbert space with the system size. On the other side, in avoiding retrieving exact quantum many-body wavefunctions and settling instead for a statistical estimation of physical quantities, one ends up facing the sign problem [1], which also leads to an exponential scaling of simulation times. The sign problem constitutes as the main hurdle that prevents systematic extraction of solutions of quantum many-body systems. It permeates a variety of fields, ultimately having a central impact on materials science, quantum chemistry and quantum field theory, as well as ultracold atoms and quantum computation. Thus, greater insight into the sign problem has important implications across these many disciplines.
Apart from some special (albeit important) limits such as the half-filled fermion Hubbard model [2], the latter ‘wall’ appears to be a generic (unavoidable) characteristic of quantum Monte Carlo (QMC) methods for fermionic and frustrated bosonic systems, and is conjectured to be NP-hard [3]. In practice, the common lore that permeates the application of QMC methods to quantum many-body systems dictates that once a sign problem occurs, that is, negative weights are obtained in the course of importance sampling, there is not much one can do, and moving to other techniques are deemed a better use of resources. Yet, recent progress in quantum many- body problems is the investigation of situations in which the sign problem can be alleviated [4] , eased [5] or mitigated [6] . Since the problem is known to be NP-hard, these approaches, although very interesting, just systematically delay the main bottleneck. If one lowers the temperature, increases the lattice size or enters a (typically more realistic) regime of parameters that is more prone to display large quantum fluctuations, the sign problem will reappear.

Figure 1: The SU(2) Hubbard model on the honeycomb lattice. In the limit that the temperature T→ 0 the thermodynamic limit is achieved (L→ ∞) and the chemical potential is introduced as a perturbation μ→ 0⁺, the sign problem is worse at the critical point Uc/t 3.8, separating the Dirac semi-metal from the antiferromagnetic Mott insulator. Adapted from Science 375, 418 (2022).
Faced by these difficulties, Prof. Rubem Mondaini (CSRC), together with his postdoc Sabyasachi Tarat (CSRC), collaborated with Prof. Richard Scalettar (University of California, Davis) to try a different approach that challenges the current paradigm: Instead of facing it as a hurdle, one can use the sign problem in determinant quantum Monte Carlo (DQMC) simulations as a tracker of quantum critical behavior. This demonstration (published in Science [7]) was done via the study of a number of fundamental models of condensed matter physics, all of whose critical properties are relatively well understood.
In particular, one of the models they studied was the SU(2) honeycomb Hubbard model (see Fig. 1A),
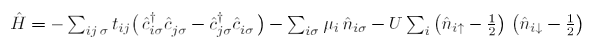
which exhibits a quantum critical point separating the Dirac semi-metal to a antiferromagneitc Mott insulator at the ratio of the interactions to the hopping energy 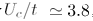 , for simulations at half-filling
, for simulations at half-filling  . As there is no sign problem at this electronic occupation, a sign problem can be revealed by inserting a small perturbation
. As there is no sign problem at this electronic occupation, a sign problem can be revealed by inserting a small perturbation  . In this case, in approaching the thermodynamic limit
. In this case, in approaching the thermodynamic limit ![]() , and the ground state regime
, and the ground state regime ![]() for an infinitely small sign-inducing perturbation,
for an infinitely small sign-inducing perturbation,  , one can reveal the quantum critical point by the interaction strength at which the sign problem emerges [see Fig. 1B and 1C].
, one can reveal the quantum critical point by the interaction strength at which the sign problem emerges [see Fig. 1B and 1C].
Generalizing such rationale for other Hamiltonians, as the U(1) honeycomb Hubbard model, and the SU(2) Ionic Hubbard model, Prof. Rubem Mondaini and his co-authors argue this phenomenon to be generic: if not protected by some symmetry of the problem, the sign problem appears in the regime of large quantum fluctuations, signaling quantum critical behavior. Ongoing research states that this is not a qualitative aspect of the sign problem but rather that the sign problem may quantitatively reveal aspects about the criticality of the transitions and the associated universality classes.
References:
[1] E. Loh, J. Gubernatis, R. Scalettar, S. White, D. Scalapino, and R. Sugar, “Sign problem in the numerical simulation of many-electron systems”, Phys. Rev. B 41, 9301 (1990).
[2] J. E. Hirsch, “Two-dimensional Hubbard model: Numerical simulation study”, Phys. Rev. B 31, 4403 (1985).
[3] M. Troyer and U.-J. Wiese, “Computational complexity and fundamental limitations to fermionic quantum Monte Carlo simulations”, Phys. Rev. Lett. 94, 170201 (2005).
[4] Jan-Lukas Wynen, Evan Berkowitz, Stefan Krieg, Thomas Luu, and Johann Ostmeyer, “Machine learning to alleviate Hubbard-model sign problems”, Phys. Rev. B 103, 125153 (2021)
[5] Dominik Hangleiter, Ingo Roth, Daniel Nagaj, and Jens Eisert, “Easing the Monte Carlo sign problem” Science Advances Vol. 6, no. 33, eabb8341 (2020)
[6] Ryan Levy and Bryan K. Clark, “Mitigating the Sign Problem through Basis Rotations”, Phys. Rev. Lett. 126, 216401(2021)
[7] R. Mondaini, S. Tarat, R. Scalettar, “Quantum critical points and the sign problem” Science 375 (6579), 418-424 (2022)



