Many linear (or linearised) problems of mathematical physics can be written as a first order system of the form

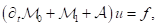
where 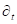 is the time-derivative,  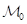and  are selfadjoint bounded operators and  is a skew-selfadjoint, possibly unbounded operator that contains spatial derivatives like div, grad and curl.
In [1] a solution theory for above systems was developed and extended later to larger classes of problems. Classical models like wave-, heat-, reaction-diffusion-, acoustics, elasticity or Maxwell's equations all fall into this class, but also models that change their type within the domain.
We will consider in this talk variational discretisation methods for this class of problems, more precisely discontinuous [2] and continuous [3] FEM for time and space, and present a-priori convergence results.
An application of the theory will be within homogenisation of layered media, where hyperbolic and parabolic type problems are changing rapidly within one model, see e.g. [4,5].

Dr. Sebastian Franz obtained his PhD in Mathematics at the University of Technology Dresden, Germany, in 2008 and completed his Habilitation in 2014 also at the University of Technology Dresden, both on topics of singularly perturbed partial differential equations. He has been a post-doc at the University of Limerick in Ireland from 2009-2011 under supervision of Dr. Natalia Kopteva working on a-posteriori error estimation for singularly perturbed problems. Coming back to Dresden he was a substitute professor for two years there and one at University of Cottbus in Germany for another half a year. Now he has a permanent position as assistant professor/lecturer equivalent at the University of Technology in Dresden. The main focus of his research are time-dependent problems and the first order systems of evolutionary type.