提取量子多体系统的无偏差属性暴露了通过经典计算机进行数值模拟探究量子性质时面临的挑战。粗略地说，陷入了指数发散的约束之中。一方面，希尔伯特空间的维度随系统的尺寸呈指数式增长；另一方面，为避免精确检索量子多体系统的波函数而改为对物理量进行统计估计时又面临着符号问题，导致计算所需时间呈指数增长。符号问题作为系统性研究量子多体体系的主要瓶颈遍布于各个领域，并对材料科学、量子化学和量子场论，以及超冷原子和量子计算领域产生深远的影响。因此，深入地探究符号问题对众多学科具有重要的意义。
除了一些特殊模型（比如半满的费米子-哈伯德模型[2]），符号问题似乎是量子蒙特卡罗方法（QMC）处理费米子系统和受阻挫的玻色子系统的普遍特征。事实上，将量子蒙特卡罗方法应用于量子多体系统的过程中，符号问题指在重要性抽样过程中出现负机率，对于这种情况通常只能寄希望于其他手段。然而，量子多体问题的最新研究进展集中于如何避免或者缓解符号问题 [4, 5, 6]。纵然这些方法非常有趣，但其并没有从根本上解决符号问题。如果降低温度，增大系统尺寸或者研究更实际的具有强量子涨落的参数区间，符号问题将再次显现。
基于这些困难，北京计算科学研究中心的Rubem Mondaini研究员及博士后Sabyasachi Tarat 与 美国加州大学戴维斯分校Richard Scalettar 教授合作尝试了一种挑战当前范式的不同方法：将行列式量子模特卡罗模拟中的符号视为量子临界行为的追踪器，而不是作为一个障碍。该项工作（发表在《科学》杂志 [7]）研究了凝聚态物理中的几个基本模型，对这些模型的关键特性给予了很好的理解。
特别地，他们研究了蜂窝晶格中具有SU(2) 对称性的哈伯德模型，如图1A。其哈密顿量为
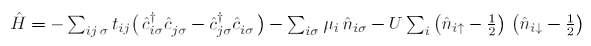
在半满时存在一个由相互作用导致的从狄拉克半金属到反铁磁模特绝缘体的量子临界点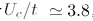 
。虽然在此电子占据数下没有符号问题，可通过引入微下的扰动来揭示符号问题 (
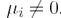)。当接近热力学极限情况（
）和无限小符号导致的扰动的基态时，可通过符号问题表现的强度来揭示量子临界点，如图1（B, C）。
Rubem Mondaini 研究员和他的合作者将这种现象推广到其他模型，如蜂窝晶格中具有U(1) 对称性的哈伯德模型和正方晶格中具有SU(2) 对称性的ionic-Hubbard模型：如果没有受到某些对称性的保护，符号问题出现在量子涨落很强的区域内，这一现象预示着量子临界行为。正在进行的研究表明，这不仅是符号问题的定性方面，并且符号问题可以定量地揭示有关相变的临界行为和普适类的性质。
图1：蜂窝晶格中具有SU(2) 对称性的哈伯德模型。在温度趋于零T→0以及系统尺寸趋于热力学极限的情况下L→∞，化学势作为一个正向的微扰被引入μ→0+，符号问题在临界点Uc/t=3.8处最严重，刚好可以将狄拉克半金属相和反铁磁绝缘相区分开。图片来源：Science 375, 418 (2022)
参考文献：
[1] E. Loh, J. Gubernatis, R. Scalettar, S. White, D. Scalapino, and R. Sugar, “Sign problem in the numerical simulation of many-electron systems”, Phys. Rev. B 41, 9301 (1990).
[2] J. E. Hirsch, “Two-dimensional Hubbard model: Numerical simulation study”, Phys. Rev. B 31, 4403 (1985).
[3] M. Troyer and U.-J. Wiese, “Computational complexity and fundamental limitations to fermionic quantum Monte Carlo simulations”, Phys. Rev. Lett. 94, 170201 (2005).
[4] Jan-Lukas Wynen, Evan Berkowitz, Stefan Krieg, Thomas Luu, and Johann Ostmeyer, “Machine learning to alleviate Hubbard-model sign problems”, Phys. Rev. B 103, 125153 (2021)
[5] Dominik Hangleiter, Ingo Roth, Daniel Nagaj, and Jens Eisert, “Easing the Monte Carlo sign problem” Science Advances Vol. 6, no. 33, eabb8341 (2020)
[6] Ryan Levy and Bryan K. Clark, “Mitigating the Sign Problem through Basis Rotations”, Phys. Rev. Lett. 126, 216401(2021)
[7] R. Mondaini, S. Tarat, R. Scalettar, “Quantum critical points and the sign problem” Science 375 (6579), 418-424 (2022)
